생존분석 - Survival Function의 차이 Log-Rank Test
의학에서 어떤 treatment 가 2개그룹의 생존확률에 유의미한 영향을 주는지 알고 싶은 경우는 흔하게 있습니다.
H0 : S1(t) = S2(t) for all t, 이 hypothesis를 Lifetest 를 이용하여 그룹간 생존확률의 차이가 있는지 Log-Rank, Wilcoxon Test 통해 수행할 수 있습니다.
< SAS Code >

1) 모든 테스트 결과 보기
ods graphics on;
proc lifetest data=surv_test plots=s(TEST);
time futime*cens(0);
strata treat/tests=all;
run;
ods graphics off;
* futime : time 변수
* cens : censored 여부가 있는 변수, ( ) 안의 숫자는 cens 변수의 값으로 censored data를 나타냅니다.
( 0 for censored data, 1 for uncensored data )
* plots=s(TEST)는 Survival plot에 Log-Rank test p-value를 함께 보여줍니다.
* strata 구문에 의해서 2개의 treat (1과2)에 따라 생존확률의 차이를 구해줍니다.
* tests=all 옵션은 가능 모든 test 결과를 보여줍니다.
(Log-Rank, Wilcoxon, Likelihood-ratio Test와 nonparametric tests인 Tarone-Ware, Peto-Peto, Modified Peto, Flaming-Harrington test 결과를 모두 보여줍니다.)
* tests=all 옵션없이 strata treat 만 사용하면 Log-Rank, Wilcoxon test 결과만 보여줍니다.
2) Log-Rank, Wilcoxon test 결과만 보기
ods graphics on;
proc lifetest data=surv_test plots=s(TEST);
time futime*cens(0);
strata treat;
run;
ods graphics off;
< SAS Output >
SAS Output은 Log-Rank, Wilcoxon 결과에 대한 설명입니다.

* Test of Equality over Stata 의 결과에서 p-value는 모두 0.05보다 작아서, null hypothesis 기각을 하지 못합니다. 즉, treat 그룹간 생존확률의 차이가 유의하게 없습니다.
* -2Log(LR)은 likelihood-ratio test 결과로 hazard 확률이 strata 간에 일정해야한다는 가정을 만족해야 하는 조건이 있어서 Log-Rank, Wilcoxon test 보다 덜 사용하는 test입니다.
* Log-Rank, Wilcoxon Chi-square statsitcs = (Rank Statistics**2)/Covariance 로 계산됩니다.
( ex. Log-Rank Chi-square statistics=1.3126 = (-2.3376)**2/4.16301 )
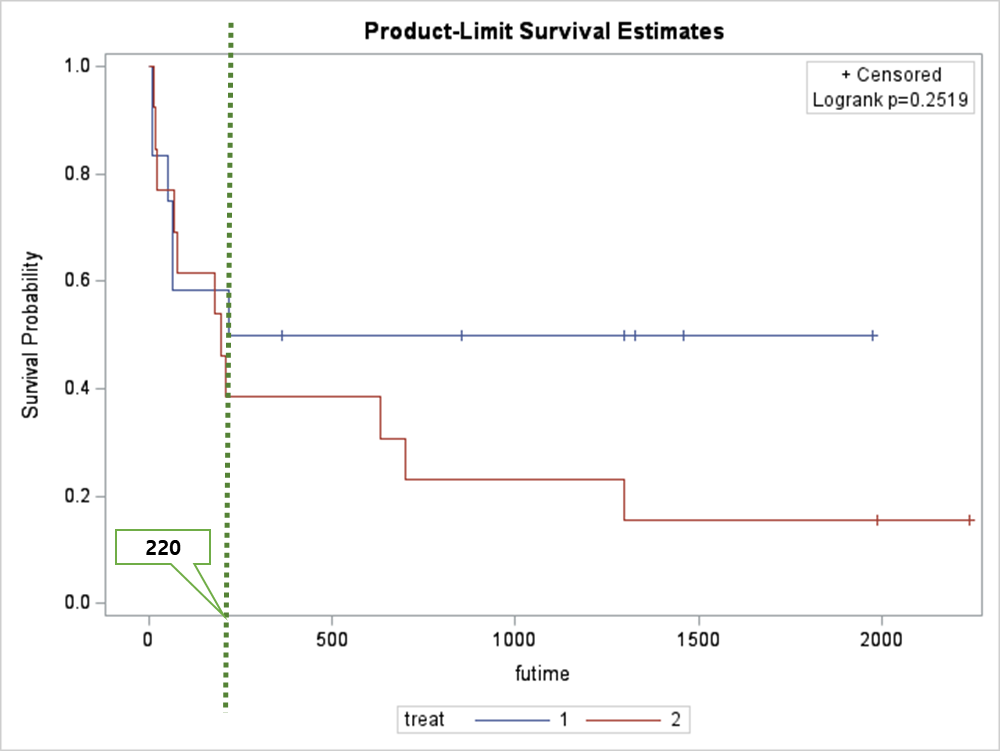
* futime 에서 220(days) 이전은 treat 2그룹간 차이가 사각적으로도 없습니다.
* 220(days) 이후에서 treat=1 그룹의 생존확률은 동일합니다.
▶ Log-Rank test 는 S1(t) = [S2(t)]**r ( r≠1) 인 경우를 테스트하는데 적합니다. 즉, 두 그룹에서 한 그룹의 생존확률이 비례적인 증감을 테스트하는 proportional hazards model 에 적합합니다.
▶Wilcoxn test 는 event time 이 log-normal distribution (두그룹간에 variance는 동일하고, mean은 다를때)인 경우 적합합니다.
▶Log-Rank, Wilcoxon 두가지 test 모두 생존곡선이 서로 만날때(cross)는 그 차이를 test하기는 어렵습니다.
다음으로, 그룹간 생존확률의 차이가 나는 예제입니다. 동일한 테이터셋을 이용하여 group을 renal (0/1) 변수를 이용해 생존분석을 해보겠습니다. renal=0 은 정상기능 신장, renal=1은 손상된 신장기능을 의미합니다.
< SAS Code >
ods graphics on;
proc lifetest data=surv_test plots=s(TEST);
time futime*cens(0);
strata renal;
run;
ods graphics off;
< SAS Output >
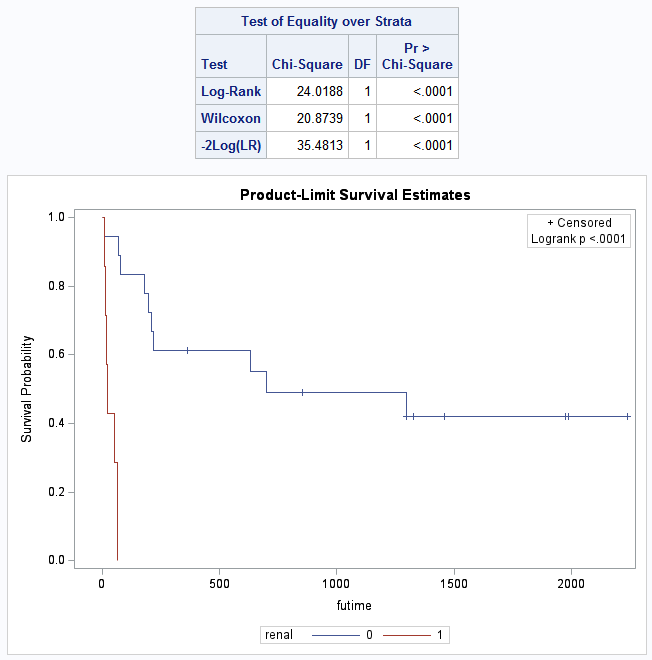
* renal=0 (파란색) 즉, 정상기능 신장그룹의 생존확률은 서서히 떨어집니다.
* renal=1 (빨간색) 즉, 손상 신장그룹의 생존확률은 초기에 급격하게 떨어집니다.
* Log-Rank,WilCoxon, Likelihood-ratio test 모두 2 그룹간 차이가 유의하게(p<.0001)있음을 보여줍니다.
'의학통계 > 통계분석' 카테고리의 다른 글
| 생존분석 - Kaplan-Meier Method 기초 (0) | 2022.07.07 |
|---|---|
| 매개효과 분석 - Mediation (0) | 2022.06.24 |
| 공분산분석 - ANCOVA (Analysis of Covariance) (0) | 2022.06.23 |
| 다중회귀모형 - Multiple Linear Regression (0) | 2022.06.22 |
| 선형회귀모형 - Linear Regression (0) | 2022.06.22 |




댓글